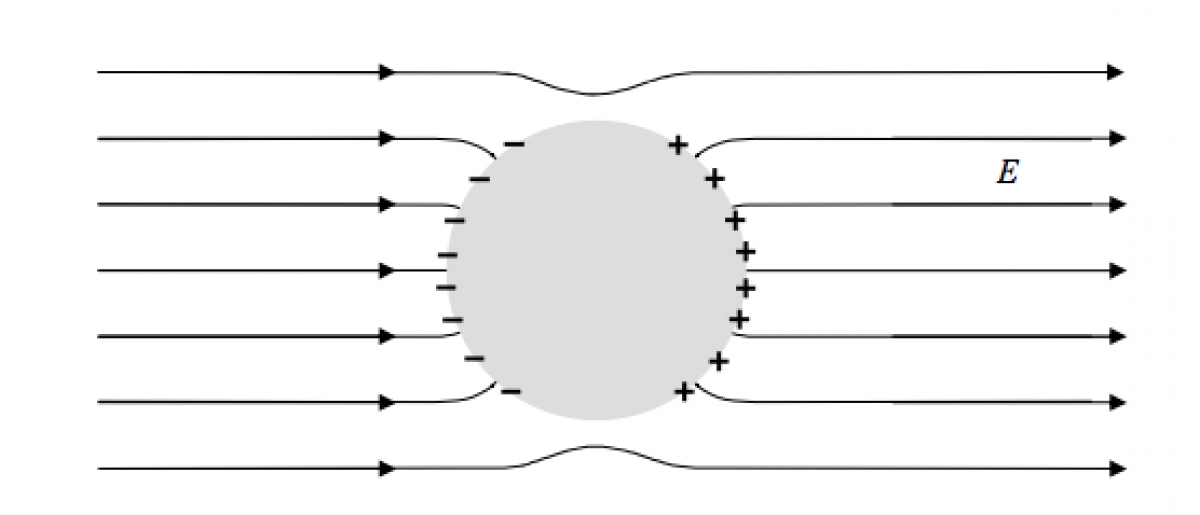
Densità di carica superficiale in un conduttore cilindrico infinito immerso in un campo elettrico uniforme
La distribuzione superficiale di carica in un conduttore cilindrico uniforme immerso in un campo elettrico costante e perpendicola
di Andrea Carpi
<h3>Tesi</h3><div>La distribuzione superficiale di carica in un conduttore cilindrico uniforme immerso in un campo elettrico $\vec{E_0}$ costante e perpendicolare al suo asse, in funzione dell'angolo $ \theta $ che le linee di campo elettrico formano con la direzione orizzontale, vale:\[ \sigma(\theta) =<br> \epsilon_0 E_0 \cos{\theta} \]</div><h3>Dimostrazione</h3><div><br><b>Definizioni</b><br><span style="letter-spacing: normal;">Presa una sezione normale all'asse del cilindro infinito nella direzione $ \hat{z} $, denotiamo con $ \hat{x}\hat{y} $ il piano che lo comprende. Definendo $\theta$ l'angolo che un punto generico $P$ appartenente al perimetro $\Gamma$ della sezione del cilindro di raggio $R$ forma con la direzione $\hat{x}$, si ha che \[ P(R\cos(\theta),R\cos(\theta)) \space \forall P \in \Gamma\] Si definiscono inoltre $ \hat{u_T} $ e $ \hat{u_N} $ i vettori rispettivamente tangenti e normali a $\Gamma$ in ogni punto $P$ di $\Gamma$.<br><br><b>Morfologia del problema<br></b><br>si consideri il campo elettrico esterno $\vec{E_0}$, esso può essere pensato come somma vettoriale delle componenti $\vec{E_{0_T}}$ tangente alla sezione del conduttore ed $\vec{E_{0_N}}$ normale alla stessa.\[ \vec{E_0} = \vec{E_{0_N}} +\vec{E_{0_T}} \] \[ \vec{E_0} = \mid\mid\vec{E_{0_N}}\mid\mid \hat{u_N}+\mid\mid\vec{E_{0_T}}\mid\mid \hat{u_T} \] Questa equazione è valida per ogni punto della superficie conduttore e quindi si ha che \[ \vec{E_0} (\theta) = \vec{E_{0_N}} (\theta) +\vec{E_{0_T}}(\theta) \space \forall \theta \in [0,2\pi] \] \[ \vec{E_0} (\theta) = E_0\cos{\theta} \space\hat{u_N} +E_0\sin{\theta} \space\hat{u_T} \space \forall \theta \in [0,2\pi] \] Per effetto del fenomeno di induzione elettrostatica, sulla superficie del cilindro si ha una carica la quale genera un campo $\vec{E_i}$ che, come è noto, è uguale ed opposto al campo $\vec{E_0}$ e dunque \[ \vec{E_0} + \vec{E_i} = \vec{0} \space \forall P \in \Gamma\] e in particolare<br></span>\[ \vec{E_0}(\theta) + \vec{E_i}(\theta)\ = \vec{0} \space \forall \theta \in [0,2\pi]\]Tuttavia è ugualmente lecito scomporre anche $\vec{E_i}$ lungo un versore tangente e uno normale: \[ \vec{E_i} = \vec{E_{i_N}} +\vec{E_{i_T}} \space \forall P \in \Gamma\] \[ \implies \vec{E_i}(\theta) = \vec{E_{i_N}}(\theta) +\vec{E_{i_T}}(\theta) \space \forall \theta \in [0,2\pi] \] e conseguentemente si ha che \[ \vec{E_{0_N}}(\theta) = \vec{E_{i_N}}(\theta) ,\space \vec{E_{0_T}}(\theta) = \vec{E_{i_T}}(\theta)\space \forall \theta \in [0,2\pi] \] <br><br><b>Annullare la componente normale</b><br>Ipotizziamo di essere già nella situazione finale, quando $\vec{E_0} = -\vec{E_i}$, e notiamo che le linee di campo al di fuori della superficie sono ortogonali alla stessa, mentre all'interno del conduttore non ve ne sono affatto. Avvicinandosi alla superficie del cilindro tanto da poterla considerare piana, è lecito applicare il teorema di Gauss a un cilindretto $A$ di raggio $r_A$.\[ \Phi_{A}(\vec{E_{i_N}}) = \Phi_{A_{base sup}}(\vec{E_{i_N}}) + \Phi_{A_{base inf}}(\vec{E_{i_N}}) + \Phi_{A_{lat}}(\vec{E_{i_N}}) \] Poichè le linee di campo sono perpendicolari alla base superiore, mentre non ve ne è alcuna ad attraversare la base inferiore, si ha che \[ \Phi_{A}(\vec{E_{i_N}}) = \mid\mid\vec{E_{i_N}} A_{base}\mid\mid = \frac{Q}{\epsilon_0} = \frac{\sigma A}{\epsilon_0} \] \[\implies \mid\mid \vec{E_{i_N}}\mid\mid = \frac{\sigma}{\epsilon_0} \implies \mid\mid \vec{E_{i_N}}(\theta)\mid\mid = \frac{\sigma(\theta)}{\epsilon_0} \space \forall \theta \in [0,2\pi] \] tuttavia, come da dimostrazione precedente, si ha che \[ \mid \mid \vec{E_{0_N}}\mid\mid = \mid\mid\vec{E_0}\mid\mid \cos{\theta} = \mid\mid\vec{E_{i_N}}\mid\mid = \frac{\sigma(\theta)}{\epsilon_0} \] \[ \implies \sigma(\theta) = \epsilon_0\mid\mid\vec{E_{0}}\mid\mid \cos{\theta} = \epsilon_0 E_{0} \cos{\theta} \]<br><b>Annullare la componente tangenziale</b><br>Una volta trovata una distribuzione di carica tale da rendere nulla la componente normale $\vec{E_{0_N}}$ di $\vec{E_0}$, occorre dimostrare che questa stessa distribuzione di carica è tale da annullarne anche la componente tangenziale $\vec{E_{0_T}} = E_0\sin{\theta} \space \hat{u_T}$ e quindi verificare che vale $- \vec{E_{i_T}}$.<br>Valutiamo ora solo il campo $\vec{E_i}$ generato per l'effetto del fenomeno di induzione elettrostatica e consideriamo unicamente quest'ultimo ai fini della dimostrazione.<br>Poichè la carica non è distribuita uniformemente lungo $\Gamma$ e dunque lungo il cilindro infinito, avremo zone con una carica maggiore e altre con una carica relativamente minore e potremo considerare queste differenze di carica come a tutti gli effetti dei dipoli infinitesimi che, intuitivamente, genereranno un campo elettrico. https://www.wearestudents.it/post/php/getUploadedMedia.php?tkn=CJYraxHdbG5adc312cd52ff&mime=image%2Fjpeg
Una volta definiti $ \vec{E_{i_N}}(\theta + \delta)$ e $\vec{E_{i_N}}(\theta)$, e con $\vec{E_{punte}} $ ed $\vec{E_{origini}}$ le congiungenti delle loro punte e delle loro origini, è palese verificare che \[ \vec{E_{punte}} (\theta)= \vec{E_{i_N}}(\theta + \delta) - \vec{E_{i_N}}(\theta) - \vec{E_{origini}} \] Essendo le origini appartenenti a $\Gamma$, il vettore $\vec{E_{origini}}$ ha per modulo la distanza tra due punti appartenenti ad una circonferenza, e per piccoli angoli $\delta$ questa distanza può essere approssimata all'arco di curva compreso tra i due punti, in formule: \[\mid\mid \vec{E_{origini}}\mid\mid \sim R \delta \space \delta \space \text{piccolo} \] quindi, per $\delta \to 0$, $\mid\mid \vec{E_{origini}}\mid\mid = R\delta= \vec{0}$. Facendo riferimento all'equazione di cui poco sopra e ricordando che per dimostrazione precedente vale \[\vec{E_{i_N}}(\theta) = \frac{\sigma(\theta)}{\epsilon_0} \hat{u_N}= \frac{\epsilon_0 E_{0} \cos{\theta}}{\epsilon_0} \hat{u_N}= E_{0} \cos{\theta} \space\hat{u_N}\] è dunque possibile considerare $\vec{E_{i_N}}(\theta)$ come il campo tangete originato da un incremento infinitesimo in quello normale: \[ \vec{E_{i_T}} = \vec{E_{punte}}(\theta) = \lim_{\delta \to 0} \frac{\vec{E_{i_N}}(\theta + \delta) - \vec{E_{i_N}}(\theta)}{\delta} \] \[ \vec{E_{i_T}}(\theta)<br> = \lim_{\delta \to 0} \frac{E_0 [\cos{(\theta+\delta)} - \cos{\theta}]\space\hat{u_N}}{\delta} = - E_0 \sin{\theta}\space\hat{u_T} \] che ha un segno negativo poichè ha verso opposto a quello considerato in partenza, ovvero il campo indotto tangente ha la medesima direzione di $\vec{E_{0_T}}$ ma verso opposto, quindi \[ \vec{E_{0}}(\theta) = \vec{E_{0_T}}(\theta)+\vec{E_{0_N}}(\theta) = E_0\cos{\theta}\space\hat{u_N} + E_0\sin{\theta}\space\hat{u_T} =\] \[ = - \vec{E_{i_T}}(\theta)+-\vec{E_{i_N}}(\theta) = -\vec{E_{i}}(\theta) \] \[ \implies \vec{E_{0}}(\theta) = -\vec{E_{i}}(\theta) \space\forall P \in \Gamma \] Q.e.d. </div>