De Stadialibus
Il Teorema dei numeri Stadiali è un teorema di matematica che stabilisce una relazione tra lo sviluppo di una serie numeric
di Andrea Carpi
15 min
<h3>Enunciato</h3>
Se n è un numero naturale positivo qualsiasi, il valore della sommatoria della parte intera delle radici da $1$ ad $n$ con $n ∈ N$ è numericamente uguale al volume del cubo che ha per lato $(n+1)$ diminuito della sommatoria dei quadrati da $1$ ad $(n+1)$.<h3><br></h3><h3>Dimostrazione<br></h3><div>
Caso $n$ predecessore di un quadrato perfetto
Sia $S$ la somma così definita:
\[ \sum\limits_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6} \]
$S= \sum_{k=1}^{N}{\sqrt{{2}{k}}=[{\sqrt[{2}]{1}}]+[{\sqrt[{2}]{2}}]+[{\sqrt[{2}]{3}}]+[{\sqrt[{2}]{4}}]+[{\sqrt[{2}]{5}}]+...+[{\sqrt[{2}]{n-1}}]+[{\sqrt[{2}]{N}}]} $
$S=1+1+1+2+2+...+[\sqrt[{2}]{n}]$
Posto $n=[\sqrt[{2}]{n}]$, non è difficile convincersi che $n$. Dunque:
$ S=(1*3)+(2*5)+...+(n*(2n+1))=\prod _{k=1}^{N}(k*(2k+1))$
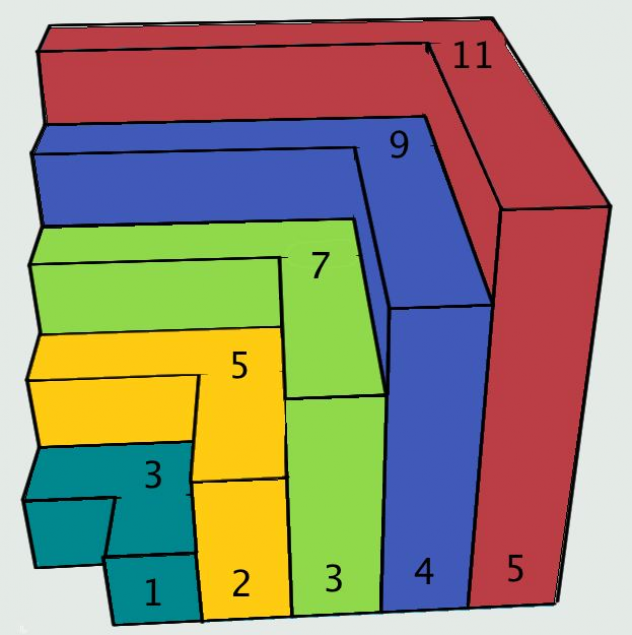
Essendo noto che la successione delle differenze fra due quadrati perfetti consecutivi è la successione dei numeri dispari positivi, è lecito pensare i termini $(2k+1)$ della successione come in FIGURA 1.
Si prosegua moltiplicando tali figure per il corrispondente fattore indicato nel simbolo di produttoria. Si ha dunque che la configurazione spaziale della figura così ottenuta è quella di FIGURA 2.
https://www.wearestudents.it/post/php/getUploadedMedia.php?tkn=EbaPTDNlX95ad28255da6ab&mime=image%2Fjpeg
Il volume del medesimo solido può essere calcolato come tagliando la figura a fette. Si ottengono dunque figure il cui volume, considerata arbitrariamente l'altezza $Z$ unitaria, è quello di parallelepipedi di dimensioni:
$(X,Y,Z)=(n+1,n+1,1)-(a,a,1)=(N,N,1)-(a,a,1)$, dove $N=n+1$.
Segue che il volume totale della figura, che corrisponde al valore della serie numerica $S$ quando $N$ sia il $N$ il predecessore intero di un quadrato perfetto, vale:
\[ V = S(N) = \prod_{k=1}^{N}((x,x,1)-(x,x,1))= \]
\[ N^3-(1^{2}+2^{2}+3^{2}+4^{2}+...+({N-1}^{2})+N^{2}) \]
\[V=S(N)=N^3-\sum_{k=1}^{N}k^2 \]
Noto il valore di \[ \sum_{k=1}^{N}[k^{2}]={\frac {N*(N+1)*(2N+1)}{6}} \] \[ V=S(N)=N^3-\frac {N*(N+1)*(2N+1)}{6} \]<br><br>
<h3>Caso generale</h3><br>
Poichè ogni numero intero positivo maggiore di zero si può esprimere come la somma del quadrato perfetto minore ad esso più vicino $x^{2}$ più la differenza tra il numero di partenza e il quadrato $N-x^{2}$:
\[ x^{2}\leq [{\sqrt[{2}]{n}}]\leftrightarrow N=x^{2}+(N-x^{2}) \] con $ x=[{\sqrt[{2}]{n}}]$, ovvero la parte intera della radice quadrata di $n$.
Segue che:
\[ \sum_{k=1}^{N}[{\sqrt[{2}]{k}}]=\sum_{k=1}^{[{\sqrt[{2}]{x}}^{2}]}[{\sqrt[{2}]{k}}]+(x)(N-x^{2}) \]
Dal momento che se N non è un quadrato perfetto, allora il valore della sommatoria della parte intera delle sue radici quadrate da $1$ ad $N$ è equivalente a quella delle radici fino ad uno meno il quadrato perfetto minore di $N$ a lui più vicino $(x^{2}$, dove $x=\sqrt {n}$ incrementato del valore della radice di tale quadrato per $ N-x^{2}$ volte. E conseguentemente incrementato di $ x+x(N-x^{2})$.
Quindi:
\[ \sum _{k=1}^{N}[{\sqrt[{2}]{k}}]=\sum _{k=1}^{[{\sqrt[{2}]{x}}^{2}]}[{\sqrt[{2}]{k}}]+(x)(N-x^{2})= \] \[ ={x^{3}-{\frac {x*(x+1)*(2x+1)}{6}}}+x+(x)(N-x^{2})= \] \[ x^{3}-{\frac {x*(x+1)*(2x+1)}{6}}+x-x^{3}+xN= \] \[ x(N+1)-{\frac {x*(x+1)*(2x+1)}{6}} \]<br>Q.e.d.<br>
<h3>Storia</h3>
Il Teorema dei numeri Stadiali è stato pubblicato per la prima volta il 7 giugno 2014 su Accademia.<br>
<h3>Bibliografia</h3>
<i>1_ Manuale di Matematica di Murray N.Spiegel pg 107, 19.3